Duder's Blog

尝试将MATLAB种最基础的功能通过C++方法实现

已知矩阵A，B

$A = \left[ \begin{matrix} A_1 \\ A_2 \\ A_3 \\ \end{matrix} \right] = \left[ \begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{matrix} \right] \tag{1}$

$B = \left[ \begin{matrix} B_1 \\ B_2 \\ B_3 \\ \end{matrix} \right] = \left[ \begin{matrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \\ \end{matrix} \right] \tag{2}$

C = A*B’

$C = A*B'= \left[ \begin{matrix} A_1*B_1 & A_1*B_2 & A_1*B_3 \\ A_2*B_1 & A_2*B_2 & A_2*B_3 \\ A_2*B_1 & A_3*B_2 & A_3*B_3 \\ \end{matrix} \right] = \left[ \begin{matrix} a_{11}b_{11}+a_{12}b_{12}+a_{13}b_{13} & a_{11}b_{21}+a_{12}b_{22}+a_{13}b_{23} & a_{11}b_{31}+a{12}b_{32}+a_{13}b_{33} \\ a_{21}b_{11}+a_{22}b_{12}+a_{23}b_{13} & a_{21}b_{21}+a_{22}b_{22}+a_{23}b_{23} & a_{21}b_{31}+a{22}b_{32}+a_{23}b_{33} \\ a_{31}b_{11}+a_{32}b_{13}+a_{33}b_{13} & a_{31}b_{21}+a_{32}b_{22}+a_{33}b_{23} & a_{31}b_{31}+a{32}b_{32}+a_{33}b_{33} \\ \end{matrix} \right] \tag{3}$

编写代码

#include<iostream>
#include<vector>
using namespace std;

void output(vector<vector<int>> vec);
vector<vector<int>> MatrixMultiplication(vector<vector<int>> vec1, vector<vector<int>> vec2);
int PartMatrix(vector<int> v1, vector<int> v2);

int main()
{
	int m1, n1, m2, n2;
	vector<vector<int>> vec1;
	vector<vector<int>> vec2;
	vector<int> v; // 存放临时数组
	int temp;

	cout << "输入矩阵A尺寸（行，列）" << endl;
	cin >> m1 >> n1;
	cout << "输入矩阵A" << endl;
	for (int i = 0; i < m1; i++) {
		v.clear();
		for (int j = 0; j < n1; j++) {
			cin >> temp;
			v.push_back(temp);
		}
		vec1.push_back(v);
;	}

	cout << "输入矩阵B尺寸（行，列）" << endl;
	cin >> m2 >> n2;
	cout << "输入矩阵B" << endl;
	for (int i = 0; i < m2; i++) {
		v.clear();
		for (int j = 0; j < n2; j++) {
			cin >> temp;
			v.push_back(temp);
		}
		vec2.push_back(v);
	}
	cout << "输出矩阵A" << endl;
	output(vec1);
	cout << "输出矩阵B" << endl;
	output(vec2);

	cout << "计算矩阵相乘" << endl;
	vector<vector<int>> vec3;
	vec3 = MatrixMultiplication(vec1, vec2);
	output(vec3);
	
	return 0;
}

void output(vector<vector<int>> vec) {
	if (vec.empty() || vec[0].empty()) {
		// 如果数组为空，返回 (-1, -1) 表示未知
		cout << "当前数组为空" << endl;
	}
	else {
		int numRows = vec.size();
		int numCols = vec[0].size();
		for (int i = 0; i < numRows; i++) {
			for (int j = 0; j < numCols; j++) {
				cout << vec[i][j] << " ";
			}
			cout << endl;
		}
	}
}

vector<vector<int>> MatrixMultiplication(vector<vector<int>> vec1, vector<vector<int>> vec2) {
	int numRows1 = vec1.size();
	int numCols1 = vec1[0].size();
	int numRows2 = vec2.size();
	int numCols2 = vec2[0].size();

	if (numCols1 == numCols2) {
		int numRows = numRows1;
		int numCols = numRows2;
		vector<vector<int>> vec3(numRows,vector<int>(numCols));
		for (int i = 0; i < numRows; i++) {
			for (int j = 0; j < numCols; j++) {
				vec3[i][j] = PartMatrix(vec1[i], vec2[j]);
			}
		}
		return vec3;
	}
}

int PartMatrix(vector<int> v1, vector<int> v2) {
	int num1 = v1.size();
	int num2 = v2.size();

	if (num1 == num2) {
		int res = 0;
		for (int i = 0; i < num1; i++) {
			res += v1[i] * v2[i];
		}
		return res;
	}

}

运行结果

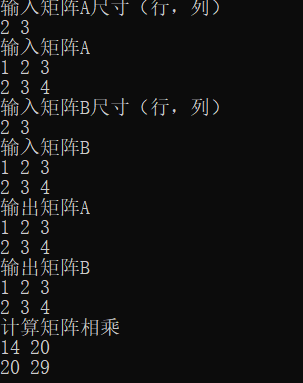
进一步优化

考虑数据类型，包含小数 复数的读取计算，以及高精度数据计算；

考虑矩阵的点乘、点除、触发运算；

考虑大矩阵的计算时间以及复杂度问题，常数将矩阵分解后再计算；