论文复现-AUC_FFL脉冲梯度方法

本文基于贾广老师文章“基于梯度的脉冲和弛豫编码”方法，复现论文中提到的AUC_FFL方法。

**“基于梯度的脉冲和弛豫编码”**这个概念最早由贾老师提出，与2022年在IWMPI上发表，《High-resolution MPI with spatially resolved measurement on field free lines》。后经过修改，完整文章发表于TMI，《Gradient-Based Pulsed Excitation and Relaxation Encoding in Magnetic ParticleImaging》。
这篇文章借用MRI成像的磁场编码概念，使用具有贾老师特色的脉冲方波激励方式实现对FFL上粒子的分离。

本文主要从三个方面介绍，分别是系统矩阵搭建、信号采集、解系统矩阵。

包括接收信号、梯形波、德拜弛豫模型、AUC面积计算等函数

代码已上传至github AUC_FFL

概念说明

Pulsed Gradient Coils

脉冲梯度线圈，通过相反电流，产生两边大中间小的磁场分布。

通过方波激励，由于实际设备限制，无法产生真实方波，因此使用固定压摆率的梯形波实现。

通过梯度脉冲激励的方式对FFL空间进行编码。依次移动梯度脉冲线圈，接收信号。

Receive Coils

接收线圈，接收粒子信号。

由于方波的激励模式，接收信号理想情况下为脉冲信号；

在梯形方波激励下产生点扩散信号；

在非绝热模型条件下，即加入弛豫模型时产生拖尾现象

本文即使用弛豫尾部下面积作为信号区分FFL上粒子分布

AUC

曲线下面积，这里有必要单独讲一下，也是这篇文章的关键点之一。

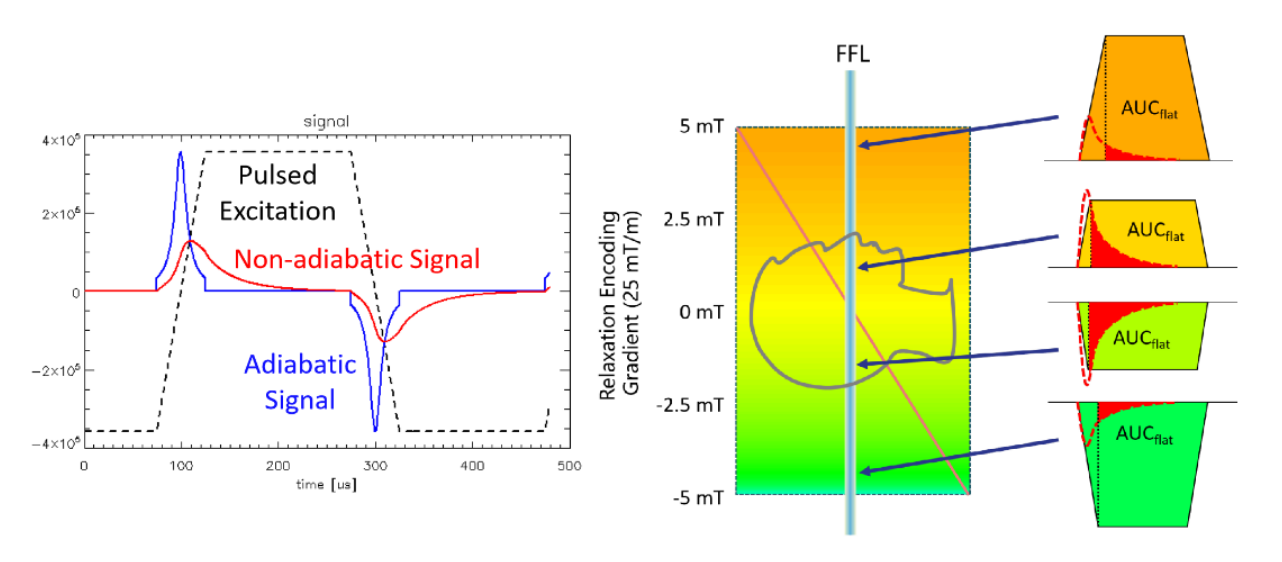
总的来说，就是由于磁粒子的弛豫效应，使得原本在梯形方波信号小表现为点扩散形状的接收信号，有长长的一条拖尾。AUC就是计算这条拖尾的面积。

因为随着激励强度的不同，磁粒子的磁化效益也不同，因此接收信号的曲线下面积(AUC)也不同，并且发现与激励强度存在相关性，因此可以根据这个关系构建出系统矩阵，进而解出粒子的浓度分布。

参数设定

fprintf('参数设定\n');
fs = 2*10^6;            	% 采样率  1.25MHz
fx = 2.5e3;             	% 激励频率 2.5kHz
Ts = 1/fs;              	% 时间间隔
Ns = round(fs/fx);      	% 单位周期采样点数
T = 1/fx;               	% 单激励周期点数
t = (0:Ts:T);               % 时间序列

EncodStep = 32;             % 离散点数
EncodY = EncodStep;          
FOVSize = [0.02,0.02];      % 成像范围
x = (-1:2/(EncodStep-1):1)*1/2*FOVSize(2);
y = (-1:2/(EncodY-1):1)*1/2*FOVSize(1);
x_move = (-1:2/(EncodStep-1):1)*1/2*FOVSize(2);
[X,Y] = meshgrid(x,y);      % 设定x和y方向位置信息

设定一些基本参数，如采样频率，激励频率，时间序列，空间大小等

脉冲梯度线圈

脉冲梯度线圈在不同位置产生不同磁场强度的

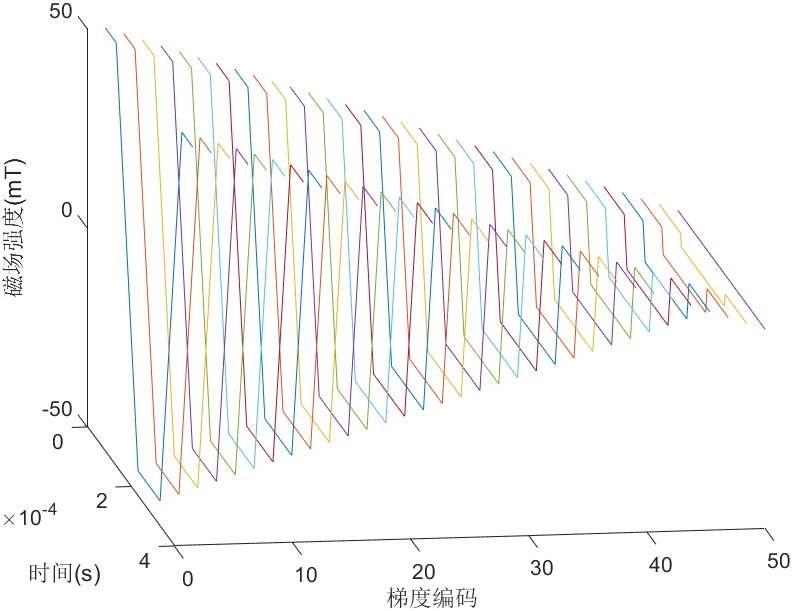
Bxmax = 25;                     % 弱梯度场(mT)
GridX = 2*Bxmax/FOVSize(2);     % 脉冲梯度(mT/m)
B_FFL_X = X*GridX;              % 脉冲梯度场(mT)

GridY = 2*Bxmax/FOVSize(1);     % 弛豫编码梯度(mT/m)
B_FFL_Y = Y*GridY;              % 移动梯度场(mT)

B_FFL = B_FFL_X + B_FFL_Y;

构建沿X轴方向的脉冲梯度，FFL线沿X方向。

使用Y轴存放移动梯度，即表示移动脉冲梯度线圈后强度。

二维矩阵数据，方便使用MATLAB矩阵加速。

B_FFL_X 、B_FFL_Y 其实都是沿着X方向的磁场强度，其中B_FFL_X 表示初始时刻梯度变化，B_FFL_Y表示移动线圈后变化多少，叠加可得到脉冲梯度强度。

方波脉冲信号

构建出空间编码的磁场强度，下一步要基于这个强度绘制出梯形波。

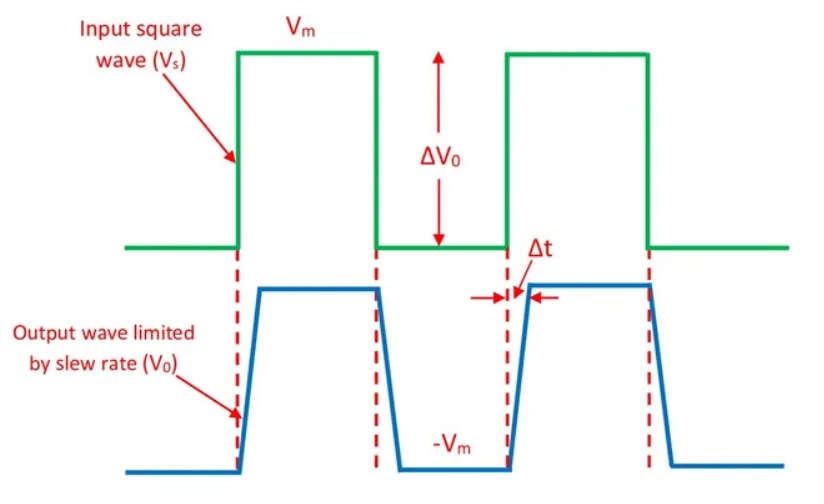
首先引出一个定义，压摆率Slew Rate。我这里为了方便仅随便设了一个数。

看到蓝色线和绿色线比较，斜着上升的蓝色线斜率就是这里的压摆率。

图像设定

这里还需要读取图像或者自己设定

方便后面计算接收信号时使用。

总结

到这一步，基本的参数设定和计算就完成了，接下来要根据不同的目的使用不同的计算过程，因此封装了几个函数使用。

下文可能用到的

基础参数：t, fs， EncodStep,

计算参数：B_FFL_wave， Map,

系统矩阵 AUCFFL_Rx

这里解释一下系统矩阵的计算

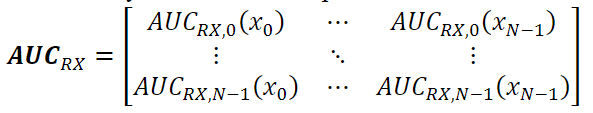
文章中对系统矩阵的定义，横坐标为每个FFL上的离散点的AUC值，AUC前文介绍过是曲线下面积，当成一个计算结构就可以。纵坐标表示脉冲梯度线圈的移动，移动一下，就要重新计算每一行FFL上不同离散点的值。

不同的离散点数据，可以看作磁粒子放置在该位置时接收的信号值。因为一次只放置一个磁粒子，因此也不需要对FFL进行求和。

这里就可以进行简化运算，我们认为所有点都放有磁粒子，并且磁粒子之间存在隔离，互相不能接收到，那这样一次矩阵运算就可以得出脉冲梯度线圈移动和FFL离散点上所有信号。

通过调用CalAUC2D函数,可以计算出曲线下面积

AUC_rx = CalCulate_AUC_RX(t,B_FFL_wave,fs);

function AUC_rx = CalCulate_AUC_RX(t,B_FFL_wave,fs)
%% 计算系统矩阵
U = receiveRX(B_FFL_wave,fs);
St = DebyeRelaxation2D(U,t);
AUC_rx = CalAUC2D(St,U);
end

信号采集 AUCFFL_Flat

$AUC_{flat} = [AUC_{flat,1}, AUC_{flat,2}, ... , AUC_{flat,N} ]$

每次计算一行的信号，以二维信号举例

AUC_flat = CalCulate_AUC_Flat_2D(t,B_FFL_wave,fs,Map);


function AUC_flat = CalCulate_AUC_Flat_2D(t,B_FFL_wave,fs,Map)
%% 计算二维接收信号
[m,n,p] = size(B_FFL_wave);
U = zeros(n,p,m);
for i = 1:m
    Mapi = repmat(Map(i,:),m,1);
    U(:,:,i) = receiveFFL(B_FFL_wave,fs,Mapi);
end
U = permute(U,[3,1,2]);
St = DebyeRelaxation2D(U,t);
AUC_flat = CalAUC2D(St,U);
AUC_flat = AUC_flat';
end

信号采集时，需要考虑FFL，即信号接收FFL上所有的粒子信号

要计算二维信号，需要移动FFL计算下一条线

计算结果的横坐标表示第几条FFL，纵坐标表示每条FFL不同的编码结果

在输入系统矩阵是要进行转置，这里已经转了。

粒子分布 AUCFFL_C

使用ART和kaczmarz方法分别解算

FFLnum = 32;%  FFL数量
[m,n] = size(AUC_rx);
C_img = zeros(FFLnum,n);
for i = 1:FFLnum
    %[C,iter] = ART(AUC_rx,AUC_flat(:,i),zeros(n,1),1e-3);
    C = kaczmarzReg( AUC_rx ,AUC_flat(:,i),100 ,1*10^-6 , 0,1,1);
    C_img(i,:) = C';
    fprintf('梯度编码FFL 第%d条\n',i);
end

结果

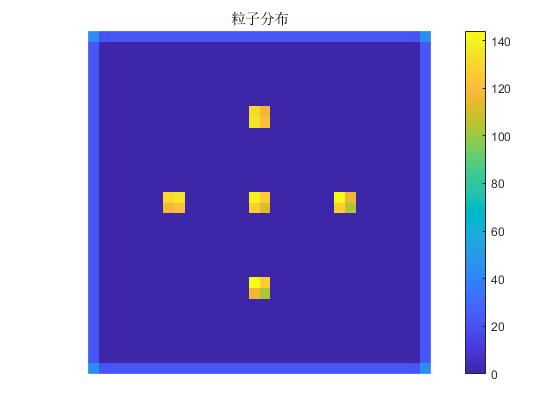
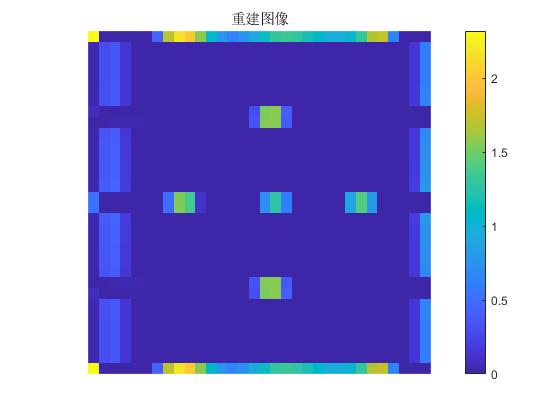
结果看上去还可以，将参数优化一下可能更好一些。

一些函数

Ladder1() 梯度方波

function wave1 = Ladder1(t,BY)
%% 用于计算相同压摆率下不同选频强度信号
fs = 1;
slewRate = 25*fs/50;       % 压摆率(mT/s)
[m,n] = size(BY);
p = length(t);      % 末尾
wave1 = zeros(m,n,p);
beginPoint = 200;
k = slewRate*1/fs;
%y = k*(x-126);
for i = 1:n
    for j = 1:m
        wave = zeros(1,p);
        A = BY(i,j);
        a = floor(-A/k+beginPoint); % 第一个点
        b = floor(A/k+beginPoint);  %
        if a<b
            flag = 1;
        else %a>b
            flag = -1;
            tmp = a;
            a = b;
            b = tmp;
        end
        wave(1:a) = -A;
        wave((a+1):b) = flag*k*(((a+1):b)-beginPoint);
        wave((b+1):((p-1)/2+1)) = A;
        tmp = fliplr(wave);
        wave(((p-1)/2+1):p) = tmp(((p-1)/2+1):p);
        wave1(i,j,:) = wave;
    end
end
end

这个地方写的有点复杂，实际上有梯形波的数学公式。

代码嘛，跑起来就行，复现文章的算法才是重点。

receiveRX()

function U = receiveRX(B,fs)
%% 计算系统矩阵
u0 = 4*pi*1e-7;     % 真空磁导率(N/A^2) (T*m/A)
S0 = 9*1e-3;        % 线圈灵敏度(T/A)
U = zeros(size(B));
Mx =MHcurve(B*1e-3);
U(:,:,2:end) = u0*S0*diff(Mx*1e3,1,3)*fs;
end

DebyeRelaxation2D()

function St = DebyeRelaxation2D(S,t)
%% 德拜弛豫
tao = 10e-6;   %s          
r = 1e-6/tao*exp(-t/tao);
r = r/sum(r);
r = [zeros(1,length(t)),r];

[m,n,p] = size(S);
for i = 1:m
    for j = 1:n
        St(i,j,:) = conv(squeeze(S(i,j,:)),r,'same');
    end
end
end

CalAUC2D()

function AUC = CalAUC2D(Sigt,Sig)
%% 用于计算AUC
[m,n,p] = size(Sigt);
index = 200:580;
AUC = zeros(m,n);
SigtR = Sigt(:,:,index);
SigR = Sig(:,:,index);
for i = 1:n %FFL上点个数
    for j = 1:m
        SigR(i,j,:) = SigR(i,j,:)./max(SigR(i,j,:),2);
        index = abs(SigR(i,j,:))<=0.1;
        AUC(j,i) = sum(SigtR(j,i,index));
    end
end
end

receiveFFL()

function U = receiveFFL(B_FFL_wave,fs,Map)
%% 计算单行FFL信号
u0 = 4*pi*1e-7;     % 真空磁导率(N/A^2) (T*m/A)
S0 = 9*1e-3;        % 线圈灵敏度(T/A)

% 循环计算每次梯度编码
[m,n,k] = size(B_FFL_wave);

U = zeros(n,k);
Mx = zeros(m,k);

for i = 1:k
    Bt = B_FFL_wave(:,:,i);
    M = MHcurve(Map.*Bt*1e-3);
    Mx(:,i) = sum(M,2);
end
U(:,2:end) = u0*S0*diff(Mx*1e3,1,2)*fs;
end

参考

Jia, Guang, Liyu Huang, Ze Wang, Xiaofeng Liang, Yu Zhang, Yifei Zhang, Qiguang Miao, et al. n.d. “High-Resolution MPI with Spatially Resolved Measurement on Field Free Lines.”
Jia, Guang, Liyu Huang, Ze Wang, Xiaofeng Liang, Yu Zhang, Yifei Zhang, Qiguang Miao, et al. n.d. “Gradient-Based Pulsed Excitation and Relaxation Encoding in Magnetic Particle Imaging.”

Duder's Blog